In this article, I am going to show you the importance of Binary Search and how to implement using Javascript. There are many articles out there talking about this algorithm, so I am not going to repeat it here.
It is also known as logarithmic search because of the time complexity O(log n) .
If you don't what time complexity means, you can check out this article to know more. In short, the time complexity is a way to find the runtime of an algorithm.
In a practical scenario, suppose you have an app with users with names from A to Z, then you are going to use a binary search algorithm starting from the middle to find the user name. By using this algorithm, you could find an element with 7 guesses from 100 items length array and that's the power of binary search.
Things to note
- Array needs to be sorted.
- After each search, the algorithm will divide the array in half.
For writing Javascript snippets, I use RunJS which is really easy to use. If you are doing coding practices, then I would suggest writing on a paper first and then Text Editor (NOT IDE).
Checking if an element exists in a sorted array
1) In-built function
let arr = [2, 3, 5, 7, 10, 20 ,22, 25, 30, 33, 34, 37, 40, 46];
let searchVal = 10;
//To check if element is present or not
console.log(arr.includes(10)) // true
//To print search value index
console.log(arr.indexOf(10)) // 4
Check this one as it talks about Binary Search vs indexOf.
2) Binary Search
function binarySearch(arr, number) {
let start = 0; // start index
let end = arr.length - 1; //array length
//LOOP until start index great than end index
while (start <= end) {
let mid = Math.floor((start + end) / 2); //middle index
if (arr[mid] == number) return true;
else if (number < arr[mid]) {
end = mid - 1;
} else if(number > arr[mid]) {
start = mid+1;
}
}
return false;
}
//Driver code
let arr = [1, 3, 4, 6, 12, 35, 40, 45, 57];
let number = 45;
binarySearch(arr, number);
As you can see from the code,
- You will have three variable start, mid & end index.
- Math.floor is used to remove floating values. JS Tip: you could also use ~~((start + end) / 2)
Useful animation
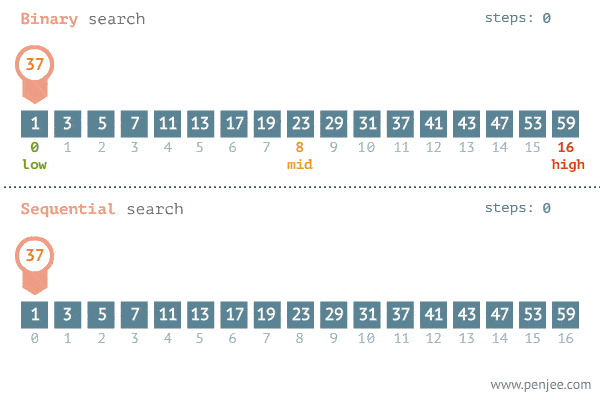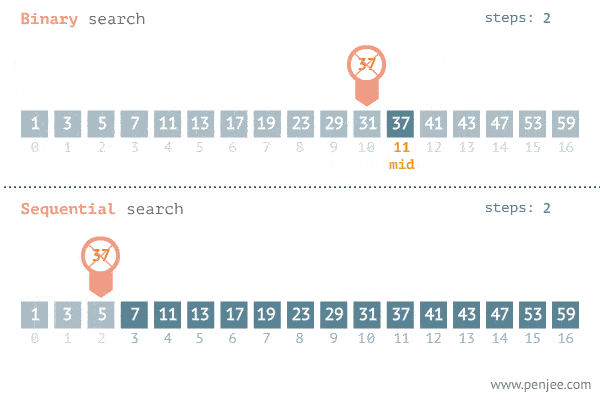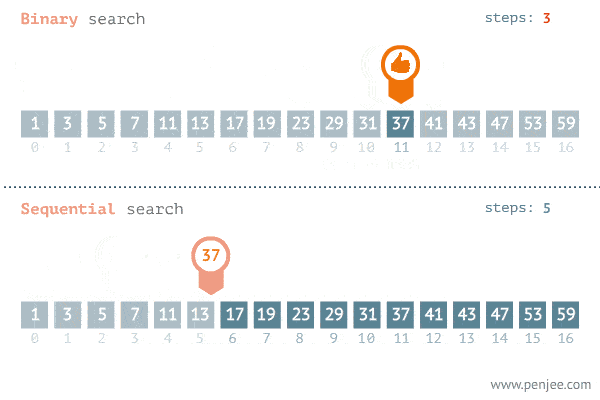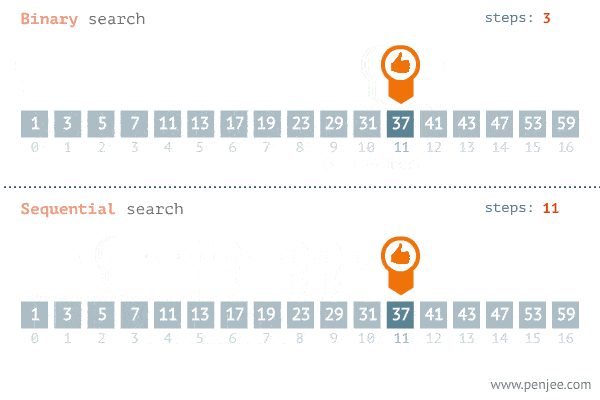
Next Step
Find the square root of a large number in O(logn) time. For example, find square root of 121. Hint: Use binary search.
If you need to add anything or found anything to update please use the comment below.
